Some history: Wilson and Lagrange
Here I have to move quickly (in fact I'll simply have to fly through this section), and attempt not to get too involved in covering standard material (of a type that I covered last November 2004 with my 2nd year BEd and BA students).
The essential point about Wilson and Lagrange is that they discovered fundamental connections
First the classic theorem of Wilson (of which there are many, many proofs, including one-and-a-half of my own (published in 1967)):
Wilson's theorem
(first proved by Lagrange in 1777). For
p
prime one has
![]() (mod
p
).
(mod
p
).
Note. The converse of Wilson's theorem:
if
![]() (mod
n
), then
n
is prime
(mod
n
), then
n
is prime
is a complete triviality (however, should polynomial time factorial modular computation ever become a reality then that would be a different matter!).
Numerical examples (here I am interested only in demonstration , not in fancy footwork; in short, I want you to see the potential size of the numbers involved).
>
p := 37; # a prime, of course
(p-1)!; # the actual value of the factorial
(p-1)! mod p; # the normal remainder
mods((p-1)!, p); # the least absolute remainder
![]()
![]()
![]()
![]()
>
p := 39; # NOT a prime
(p-1)!; # the actual value of the factorial
(p-1)! mod p; # the normal remainder
mods((p-1)!, p); # the least absolute remainder
![]()
![]()
![]()
![]()
I had to omit the large output from the (p-1)! following in the html version, as it led to problems:
>
p := nextprime(1234); # a prime
# (p-1)!; # the actual value of the factorial
(p-1)! mod p; # the normal remainder
mods((p-1)!, p); # the least absolute remainder
![]()
![]()
![]()
>
Lagrange besides publishing the first proof of Wilson's theorem in 1777, published some important related work: he proved - using Wilson's theorem - important distinctions (discovered by Fermat, who could not provide proofs) between the way in which primes leaving remainders 1 and 3 on division by 4 behaved.
Briefly, Fermat had observed (in equivalent non-congruence language ; congruence notation only came in with Gauss in his monumental Disquisitiones Arithmeticae (1801)) that
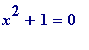 (mod
p
) has
no
solutions for prime
p
satisfying
p
= 3 (mod 4)
(mod
p
) has
no
solutions for prime
p
satisfying
p
= 3 (mod 4)
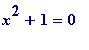 (mod
p
) has
exactly
two
solutions for prime
p
satisfying
p
= 1 (mod 4)
(mod
p
) has
exactly
two
solutions for prime
p
satisfying
p
= 1 (mod 4)
Numerical illustrations.
>
p := nextprime(1000);
p mod 4;
msolve(x^2 + 1 = 0, p);
![]()
![]()
![]()
>
p := nextprime(2000);
p mod 4;
msolve(x^2 + 1 = 0, p);
![]()
![]()
>
Suffice it to say that Lagrange noted the following (trivially-derived) consequence of Wilson's theorem:
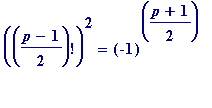 (mod
p
) (Lagrange congruence)
(mod
p
) (Lagrange congruence)
(you see why, of course? Use
![]() (mod
p
), for
(mod
p
), for
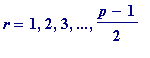 , and...)
, and...)
In summary, this is what one had
:
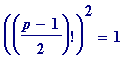 (mod
p
).
(mod
p
).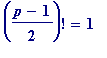 or
-1 (mod
p
), and it was a
long-standing unsolved problem
for many years to determine the sign (see Dec 15th 2004 email from Andrew Granville)
or
-1 (mod
p
), and it was a
long-standing unsolved problem
for many years to determine the sign (see Dec 15th 2004 email from Andrew Granville)
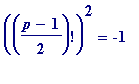 (mod
p
), from which it is easily deduced that
(mod
p
), from which it is easily deduced that
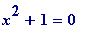 (mod
p
) has
at least
two
solutions, and a further result of Lagrange's then allowed one to conclude there were
exactly
two solutions.
(mod
p
) has
at least
two
solutions, and a further result of Lagrange's then allowed one to conclude there were
exactly
two solutions.